Zeta potential – Application trends
How does surface charge arise?
How is particle charge measured?
Methods for determining the zeta potential
Zeta potential measurement technique
Applications – possibilities for automation
The Malvern MPT-1 Autotitrator
Selected applications – an overview
Particle Characterization
There are many aspects of a particle dispersion that need to be investigated to fully characterize a system.
Particle size is often considered one of the most important parameters, however, as particle size reduces, the surface area increases significantly in comparison with the volume, so surface properties increasingly determine the dispersions characteristics.
One of the significant surface properties is the surface charge. This is an important factor in determining the interactions between particles, and hence dispersion characteristics such as dispersion stability, flocculation, viscosity, film forming characteristics etc.
The surface charge cannot be measured directly. Instead the charge at a distance from the particle, called the zeta potential is measured. This potential is usually more of interest because particles interact according to the magnitude of this value, rather than the potential at the surface of the particle.
Zeta Potential – Application Trends
The zeta potential (x), or electrophoretic mobility (µE), is increasingly being used to investigate fine particle systems.
The zeta potential is a consequence of the existence of surface charge, and can give information on electrical interaction forces between the dispersed particles. Using DLVO theory, it is possible to assess the stability of suspensions and emulsions by means of the zeta potential.
The basis of DLVO is to use the sum of the repulsive force (VR – electrostatic BORN forces) and attractive (VA – van der WAALS forces) to calculate the particle interaction potential.
VTOTAL = VR + VA
In many cases, the zeta potential can be used directly as the criterion for assessing product quality.
However stability assessment using the zeta potential as the measurable variable may only be useful if the system is sufficiently well understood.
Electrokinetic measurements can be used to investigate the effect of each of the excipients in a formulation on the dispersed materials surface characteristics. Figure 1 shows schematic examples of zeta potential Vs pH functions that are characteristic of certain surface conditions. These curves are found for example in the protolysis of acid or alkaline surface groups and in pH-dependent adsorption processes.
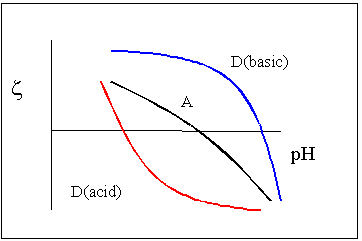
Fig. 1 Model examples of pH Vs zeta functions showing dissociation of acid or alkaline surface groups and adsorption
How Does Surface Charge Arise?
Surface charges on suspended particles can be caused by a variety of phenomena. Figure 2 shows a number of possibilities. Dissociation of functional surface groups and/or adsorption of ions are the most important processes. In many formulations the adsorption of larger molecules containing charged groups such as surfactants and polyelectrolytes play a vital role.
The surface charge of the particles is compensated in the liquid phase by counter-ions, ensuring a condition of electrical neutrality in the system as a whole.
Lattice imperfections
Surface-adsorbed ions
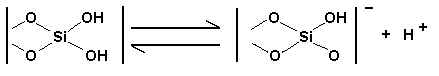
Chemical reactions on the surface
(dissociation of functional surface groups)

Adsorption or dissociation of charge-bearing molecules
Fig. 2 Examples of phenomena that lead to the development of surface charge
How is Particle Charge Measured?
The electrochemical double layer
The interface between two phases, (solid/liquid, liquid/liquid or gas/liquid) differs in a number of ways to the bulk phase. One reason for this is the different distribution of electrical charges at the phase boundary. This leads to the development of an electrical double layer with a potential different to that within either phase.
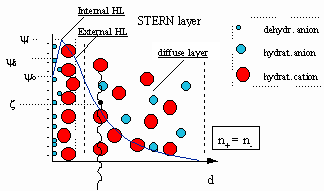
The STERN double layer model is generally used to describe the charge distribution. Figure 3 shows in schematic form the distribution at the interface for the case of a negatively charged particle surface, (yo) Charges in each phase interact. In an electrolyte solution, a monolayer is quickly adsorbed directly on the particle surface.
These are generally dehydrated ions and this region of a monolayer of ions is known as the inner Helmholtz layer.
Whether these are anions or cations depends on whether they are ‘Indifferent’ ions or ‘Specifically adsorbed’ ions.
Specifically adsorbed ions interact chemically with the surface; it could be a proton interacting with a carboxylic acid group for example. These ions can interact so strongly with the surface that they can cause charge reversal. Conversely if the ion is the same sign as the surface, the surface potential can be increased.
In the absence of specifically adsorbed ions, this inner layer consists of dehydrated or partially dehydrated counter-ions. In the case of a negative surface in contact with indifferent ions Sodium and Chloride, this would be the Sodium ion and lead to a potential (yi).
The next layer of ions (outer Helmholtz layer) are rigidly bound hydrated counter-ions, which reduce the potential to the value yd?. The internal and external Helmholtz layers form the STERN layer with thickness d. The distribution of charge carriers outside this layer, in a more diffuse region, reduces to zero in the bulk phase. Electrical neutrality ultimately exists at an infinite distance from the particle surface with n+ = n-.
Particle movements in the medium, due to for example, Brownian motion or sedimentation, leads to the concept of a shear plane within the diffuse layer. This region separates the ions associated with the particle from those in the bulk phase. The potential at this shear plane is what is referred to as the zeta potential (x).
The extent of the diffuse double layer is dependent on the ionic strength of the electrolytes and the valency of each of the ions.
Multivalent ions are particularly important. Their effect on the screening of the surface charge is related to the counter-ion valency. The flocculation concentration for divalent counter-ions is on average about 100 times lower than for monovalent ions, and for trivalent ions about 1000 less. This is known as the Schultze-Hardy rule and is the explanation for the use of Aluminium or Ferric ions to cause the flocculation of particles with negative zeta potential in water treatment plants.
Specific adsorption
The distribution of ions is more complicated if ions exhibit specific adsorption behavior. Specific ion adsorption can have a dramatic effect on particle mobility at low ion concentrations.
Figure 4 Shows how the composition of the medium can affect the surface potential and the extent of the electrical double layer. These three cases are arranged so the value of zeta potential is the same in each case. This demonstrates that the surface charge cannot be inferred from zeta potential.
It is worth emphasizing the distinction between surface potential and zeta potential. The zeta potential is the controlling parameter for particle interactions. Modifying the zeta potential requires knowledge of the potential of the surface and its chemistry.
Investigation of the interaction of ions with the surface, and their effect on zeta potential is assisted by the determination of zeta potential as a function of a number of parameters.
The parameters that it is useful to investigate are pH, conductivity and the concentration of any specifically adsorbed ions or polymers in the system.
Methods for Determining the Zeta Potential:
Electrokinetic phenomena
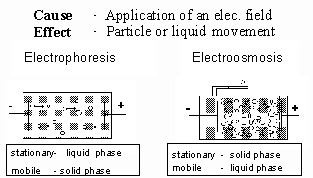
There are four electrochemical phenomena that can be used for the determination of zeta-potential, electrophoresis, electroosmosis, streaming and sedimentation potential
Electrophoresis and streaming potential are the most important commercial effects that have been exploited to determine zeta potential. The Malvern Zetasizer uses electrophoresis, however electroosmosis is an interfering effect that must be considered (Fig. 5). There are a number of ways of accounting for this effect. The use of measurements at the stationary layer is one method that is discussed in the next section.
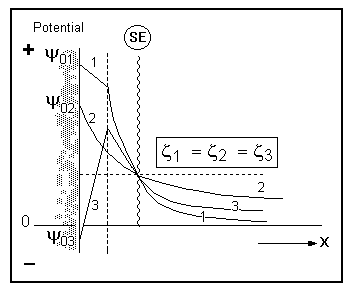
1. Positively charged particles on the surface, moderate
2. adsorption of anions, moderate ionic strength positively charged particles with no specific adsorption,
low concentration of electrolyte
3.negatively charged particles, strong specific cation
adsorption, moderate electrolyte concentration
Micro-electrophoresis
The conventional method for measuring zeta potential is to observe the migration of particles in a dispersion with a microscope and measure their velocity using a stopwatch. The current technique of laser Doppler velocimetry (LDV) has mostly replaced this laborious measurement procedure.
Both techniques are based on measurement of the migration rate of dispersed particles under the influence of an electric field. The observed velocity (v), divided by the strength of the applied electrical field (E), is a direct measure of the electrophoretic mobility (µE) of the particles examined.
v /E = µE
The zeta potential can be calculated from the mobility using the Henry equation.
Henry equation:
mE = e * x * f(k a)/6ph
e – dielectric constant of the medium, h – viscosity of the medium, f(k a) – correction factor which takes into account the thickness of the double layer and particle diameter. The unit k is a reciprocal length. 1/k is frequently described as the thickness of the double layer.
In practice an approximation can be made for f(k a), this is f(k a) = 1.0 for non-polar media,f(k a)=1.5 for particle dispersions in polar media.
f(k a) = 1.5 is a good approximation for particles >100nm in aqueous solutions with an ionic strength >10-3 M. This is known as Smoluchowski approximation:
mE = e * x /4ph
at 25%C it is simplified to x = 12.85 mE mV.
The second limiting case f(k a)=1.0 applies for very small particles in media with a low permittivity. This is known as the Hückel approximation.
If the conventional microscopic observation technique is compared with modern techniques, the advantages of the LDV methods are many. Some important advantages are:
- Statistically better measurements
- Seconds measurement time rather than 10-30 minutes
- Measurement of smaller particles, 5-10nm rather than a minimum of 200nm
- Measurement of zeta potential distributions
- Improvement in measurement repeatability due to a reduction in the Joule heating effect
- Ability to automate complex measurements (e.g. pH or concentration dependences)
The electrophoresis cell
Figure 6 shows the structure in principal of an electrophoresis cell for determining the zeta potential. It comprises a quartz glass capillary 50mm long, cross section 5mm by 2mm, with electrodes at both ends. The capillary is sealed by valves to form a closed tube.
The stationary layer
In the same way that an electrical double layer is associated with charged particles, the same structure exists at the charged capillary wall. This leads to a liquid flow in the cell due to electroosmosis. This adds a velocity to the particle mobility at all points in the cell except at a special position called the stationary layer or stationary plane. This is created in a closed capillary because of the return flow in the center of the cell. At the stationary layer the fluid flow along the cell wall is exactly cancelled by the return flow. Measurements at this position give the true electrophoretic mobility.
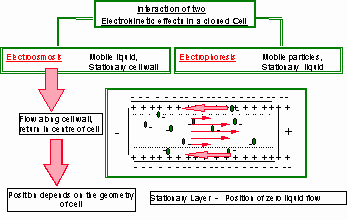
The position of the stationary plane is dependent on the cell geometry and can be calculated for symmetrical shapes of capillary.
Zeta Potential Measurement Technique
In contrast to the traditional microscope measuring technique, in the LDV method the particle image is replaced by the illumination of particles by intersecting laser beams, the observer’s eye by the photomultiplier, and the stopwatch by the correlator.
The Malvern system is called the Zetasizer. This system is available with different combinations of measured parameters. These are zeta potential, size, pH and conductivity. The features of this system are its ease of use provided by pre-aligned optics and single button measurement software.
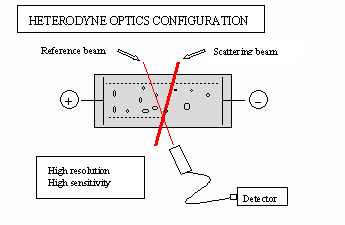
Heterodyne optics
In this optical arrangement the scattered light from particles in the measurement zone is mixed with attenuated light from the illuminating laser that is directly focused on the detector. These two beams intersect at a low angle, 12.7 degrees. (Fig. 7) This effectively increases the resolution as the effect of Brownian motion is greatly reduced at forward scattering angles. At higher angles, Brownian motion causes a problem as it ‘smears’ out the velocity spectrum, making it difficult to resolve mixtures of particles with different mobilities.
Signal processing and data evaluation
The measurement technique used is often known as Laser Doppler Velocimetry (LDV).
Moving particles in the measurement zone shift the frequency of scattered light proportional to their velocity.
The scattered light is detected by a photon counting photomultiplier and the signal input to a digital correlator. This can be thought of as simply an efficient frequency analyzer using a Fourier transform algorithm to disentangling the mobilities of perhaps thousands or millions of particles into a number of mobility channels.
As well as moving due to electrophoresis, the particles are moving due to Brownian motion. This makes the peak width broader than it should appear. To correct for this a measurement is done with no field present. The width of the peak produced will then be due only to the Brownian motion, and this width can be subtracted from the width produced by a measurement with the field applied.
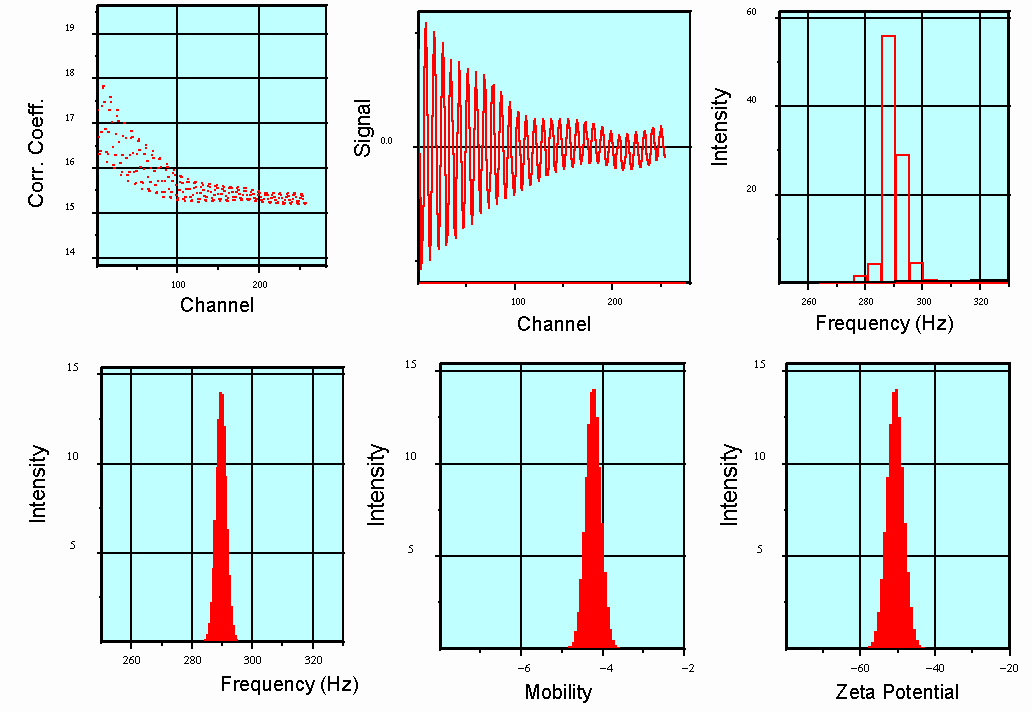
Fig. 8 Stages of signal processing from the correlation function to a Fourier Transform analysis (FFT) to frequency, mobility and zeta potential spectrum
Electrode polarization and determination of sign of the zeta potential
An alternating electrical field is used in order to exclude effects due to electrode polarization. The direction of movement of the particles is therefore periodically reversed during measurement.
In addition to this, one of the two laser beams is modulated by means of an oscillating mirror in order to determine the direction of movement and thus the sign of charge of the particle. The modulator adds a known frequency to the signal. The direction of particle movement, and therefore the sign of the charge, can be identified in this way because the frequency detected due to the particles either adds or subtracts from this modulator frequency. Figure 9 shows the time link between the direction of the electrical field and the phase of the modulated beam. With this scheme the maximum amount of data is collected with the minimum electrode polarization.
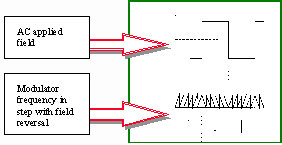
Fig. 9 Link between the applied reversing field and the phase of the modulator
A second advantage of the modulator is that particle mobilities at zero give a measured frequency, which is that of the modulator. This means that low mobility particles can be measured with the same high accuracy as particles with high mobility.
Applications – Possibilities for Automation
Properties of ultrafine disperse systems (dispersions, suspensions, and emulsions) can be examined or predicted using the zeta potential. To use this parameter, it is important to understand that the zeta potential is not a parameter of a particle alone. The zeta potential is dependent, as already discussed, on the particle and on its environment. Zeta potential data with no an exact description of the conditions under which it was measured are rarely meaningful.
Controlled changes of the environment, such as pH, that lead to modification of the zeta potential, can give important information about the nature of the particle surface and the robustness of a dispersion to changes in the parameter.
A single measurement of the zeta potential of a dispersion in a defined set of conditions is rarely useful for the purpose of characterization. Knowledge is required of how the zeta potential varies as parameters such as pH, conductivity and other factors change.
This leads to the requirement for a large number of measurements. Automation of these changes can save time and improve repeatability.
The Malvern MPT-1 Autotitrator
The MPT-1 autotitrator now enables the Zetasizer to make automated measurements of the dependence of zeta potential on pH, conductivity or any other additive.
The automation allows measurements to be repeated by specifying a standard procedure. This makes the unattended measurements less dependant on the skill of the operator and the measurement time is reduced because the measurement is started as soon as the pH is stable.
For example, a pH-dependent titration, from pH 3 to pH10, in 12 approximately equal steps is completed in about half an hour.
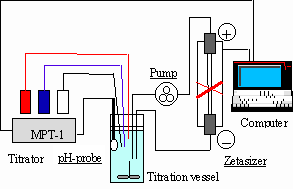
Fig. 10 Set-up of the Zetasizer with the MPT-1 autotitrator
The Autotitrator software allows a wide range of control over how the titration should proceed.
A method once developed can be stored as a standard operating procedure that can easily be recalled for a subsequent measurement.
During the titration the results can be viewed on screen as an evolving plot. The final results are presented as a report that includes all relevant information about the titration, as well as a plot and calculation of all iso-electric points detected.
Selected Applications – An Overview
Determination of optimum dispersion conditions for a wide range of applications.
Stabilization/destabilization of suspensions, dispersions and emulsions via electrostatic stabilization mechanisms.
Determination of critical coagulation concentrations, sensitivity to the concentration of additives, such as salts, surfactants, polymers.
Estimation of adsorbed polymer layer thickness.
Optimizing surface coatings, effect of surface modifications
Biological applications, characterization of erythrocytes and blood platelets, characterization of cells, bacteria etc
Characterization of material surfaces – biocompatibility
Brönsted acid-base properties of particle surfaces, significance in aqueous powder processing (ceramics, pigments, paints, varnishes, fillers etc), determination from pH-dependent trends
Lewis acid-base properties of particle surfaces, significance in non-aqueous powder processing (ceramics, pigments, paints, varnishes, polymers), determination from correlation of zeta potential with electron donation/acceptance
R. Nitzsche
Malvern Instruments GmbH, Herrenberg
M Connah
Malvern Instruments Ltd. UK